Numeric Integration using Python and Pylab

Pylab is Python module that contain NumPy and MatPlotlib.

Let f(x) = x^2 and we want to integrate it from 0 to 1.

Numerically we could use square method or trapezoidal (which is almost better).

Masa Kecil

Salah satu detil dari @pitoyoamrih yang saya suka adalah cerita tentang masa kecil seorang tokoh wayang. 

Kita tahu cerita lengkap tentang masa kecil tokoh wayang jarang ada di pakem utama. Hanya beberapa yang terkenal seperti Gatotkaca dan Wisanggeni, itupun dalam lakon  carangan.

Dengan kenyataan seperti itu (atau saya yang memang tidak tahu secara tuntas pakem utama pewayangan), buku-buku Pitoyo Amrih ini menjadi semacam hiburan yang menyegarkan. 

Tentang masa kecil Karna bersama Adirata. Deskripsi watak Karna yang ambisius, nakal dan cenderung jahat kepada orang tua angkatnya menjadi pengantar yang tepat sebagai latar belakang masa dewasanya.

Permadi kecil, sebelum diusir dari istana, yang cuek cenderung sombong dan manja, tak mau membereskan busur dan tempat anak panah.

Narayana dan Kakrasana kecil di Widarakandang yang diasuh Demang Antagopa dan Nyai Sagopi.

Masa kecil para kurawa dijelaskan dengan rapi, tentang Destarata dan Gendari yang tidak pernah memperhatikan anaknya sama sekali, dan seratus saudara seumur yang tak terurus sehingga menjadikan pengantar kelakuan Kurawa saat sudah dewasa.

Masa kecil Wisanggeni mungkin sudah banyak yang tahu karena ada lakon Lahirnya Wisanggeni.

Nah saya suka cerita detil versi Pitoyo Amrih tentang masa kecil Antareja dan Antasena. 

Childhood

One of the details of @pitoyoamrih that I like is the story of the childhood of a puppet character.

We know the full story about the childhood of puppet characters is rarely in the main Pakem. Only a few are famous like Gatotkaca and Wisanggeni, and even then in the Carangan (side story).

With such a reality (or it's just me, who  don't really know the complete Pakem of Wayang ), Pitoyo Amrih's books become a kind of refreshing entertainment.

About Karna's childhood with Adirata. Descriptions of Karna's ambitious, naughty and evil tendencies to her adoptive parents became the right introduction to her adult background.

Young Permadi, before being expelled from the palace, the ignorant tended to be arrogant and spoiled, not wanting to clear the bow and place the arrow.

Narayana and small Kakrasana in Widarakandang who are raised by Demang Antagopa and Nyai Sagopi.

The kurawa's childhood is neatly explained, about Destarata and Gendari who never pay attention to their children at all, and a hundred brothers during their unkempt years, making strong background of Kurawa's behavior as adults.

Wisanggeni's childhood may have been known because there was a play about the birth of Wisanggeni.

Now I like the detailed version of Pitoyo Amrih's version of Antareja's and Antasena's childhood.

Delphi.

Still using Delphi?

Yup, it teach me about programming discipline, :)

Flappy Bird Like in Delphi

Remember the infamous Flappy Bird? Yup, I will create the program based on that algorithm.

Newton Polynomial in Python

I wrote code for this in Delphi. This time I want to rewrite it in Python based on this wiki.

I use this set of data point
(0,0)
(1,1)
(2,4)
(4,16)
(5,25)

and I use xc=3 for the test data.

It's obvious that these sets of data points have quadratic form and f(xc) must have value of 9.

The heart of code lay on this

def n(j,xc,x):
    n = 1
    for i in arange(j):
        n *= (xc-x[i])

    return n
def a(j,l,x,y):
    if j==0:
        return y[0]
    elif j-l==1 :
        return (y[j]-y[l])/(x[j]-x[l])
    else:
        return (a(j,l+1,x,y)-a(j-1,l,x,y))/(x[j]-x[l])
        

def N(xc,x,y):
    N = 0
    for j in range(len(x)):
        N += a(j,0,x,y)*n(j,xc,x)
    
    return N

Look at the function a(j,l,x,y), that's recursive function to obtain Newton divided difference value.

the whole code is this

from pylab import *

def n(j,xc,x):
    n = 1
    for i in arange(j):
        n *= (xc-x[i])

    return n
def a(j,l,x,y):
    if j==0:
        return y[0]
    elif j-l==1 :
        return (y[j]-y[l])/(x[j]-x[l])
    else:
        return (a(j,l+1,x,y)-a(j-1,l,x,y))/(x[j]-x[l])
        

def N(xc,x,y):
    N = 0
    for j in range(len(x)):
        N += a(j,0,x,y)*n(j,xc,x)
    
    return N

x = []
y = []
#initial value
x.append(0)
x.append(1)
x.append(2)
x.append(4)
x.append(5)

y.append(0)
y.append(1)
y.append(4)
y.append(16)
y.append(25)

#for testing
xc = 3

yc = N(xc,x,y)

print ''
print xc, yc
#plot
t = linspace(-7,7,100)
u = N(t,x,y)
plot(t,u)
grid(True)
show()

.


here's the graphics

with another sets of data points, I have another result
(0,0)
(1,1)
(2,4)
(4,16)
(5,25)

Disorientasi

Kadang bingung sedang membaca buku @PitoyoAmrih yang mana, saking konsistennya. Banyak cerita yang ada di buku satu, menyisip di buku lainnya. Seakan empat atau lebih buku itu sebenarnya cuma satu buku yang dijilid bukan berdasarkan urutan, namun berdasarkan tema.

Saat membaca "Antareja dan Antasena", tiba-tiba serasa baca "Wisanggeni Membakar Api" saat tiba di bagian Antasena menjadi jagung.

Juga saat membaca "Pertempuran Dua Pemanah: Arjuna-Karna" serasa membaca sisipan dari (atau malah babon) dari "Kebaikan Kurawa".

Apakah itu berarti jelek? Tidak sama sekali. Ini berarti penulis memiliki satu plot besar yang dicurahkan di berbagai buku.



Eh, tentu saja memang ada plot besar bernama pakem di pewayangan,  :).

Hal yang menarik di sini, dengan berpegang pada plot besar, buku-buku Pitoyo Amrih memiliki konsistensi yang tinggi. Baca buku yang manapun tidak akan mengalami kebingungan tentang mana yang benar karena yang diceritakan bersumber dari hal yang sama. Namun ada juga detil-detil kecil yang menarik yang memang tidak ada di pakem atau (plot besar milik Pitaya Amrih sendiri), detil-detil ini membuat cerita menjadi menyenangkan karena tidak menjadi kaku karena pakem.

Banyak buku yang menjadi  kaku karena terlalu ikut pakem, atau buku yang terlalu aneh karena tidak mempedulikan pakem sama sekali (jadinya pembaca malah mengernyit sambil mikir "Arjuna kok gini?", "Samba kok gitu?" dsb )

Ohya, saya belum baca semua buku Pitoyo Amrih, dalam proses, tetapi sudah pasti jadi pengagum  beliau, :)

Disorientation

Sometimes I confused about reading the book @PitoyoAmrih, because it's too consistent. Many stories in a book, are inserted in other books. As if four or more books were actually just one book bound not by sequence, but by theme.

When reading "Antareja and Antasena", suddenly I read "Wisanggeni Membakar" when I arrived in the Antasena-became-Corn section.

Also when reading the "Pertempuran Dua Pemanah: Arjuna-Karna" it seemed that I read the insertion from (or even the baboon) of "Kebaikan Kurawa".

Does that mean bad? Not at all. This means that the author has one large plot devoted to various books.

Uh, of course there is indeed a big plot called the Pakem (Standart Plot) in Shadow Puppet story, :).

The interesting thing here is, by holding on to the big plot, Pitoyo Amrih's books have high consistency. Read any of his books. We will not experience a confusion about what is right because the story is from the same source. But there are also interesting little details that are not in the Pakem. These details make the story fun because it does not become rigid because not strict into Pakem.

Many books are stiff because they are too gripping, or books are too strange because they don't care about The Pakem at all (so the reader frowns while thinking "Why is  Arjuna like this?", " Why is Samba like that?" Etc.)

Oh yeah, I haven't read all of Pitoyo Amrih's books, it's still in the process, but I have definitely become his admirer, :)

Newton Polinomial.

Here's code for Newton's divided differences interpolation polynomial (quite mouthful huh, :) ).

The purpose of this method is to create a function (polynomial) that passes through given set of data points.




I read data point from several edit box.

procedure TForm1.Button3Click(Sender: TObject);
var i:integer;
begin
  for i:=0 to n do begin
    x[i]:=strToFloat(kx[i].Text);
    y[i]:=strToFloat(ky[i].Text);
  end;
  xc:=strToFloat(kxc.Text);
  yc:=fn(xc);
  kyc.Text:=floatToStr(yc);
  gambarNewton;
end;

.
kx and ky is tEdit created when button1 is clicked

procedure TForm1.Button1Click(Sender: TObject);
var i:integer;
begin
  button2.Enabled:=true;
  button3.Enabled:=true;
  button4.Enabled:=true;
  button5.Enabled:=true;

  n:=strToInt(edit1.Text);
  kxc:=tEdit.Create(form1);       kyc:=tEdit.Create(form1);
  kxc.Parent:=form1;              kyc.Parent:=form1;
  kxc.Left:=36;                   kyc.Left:=72;
  kxc.Width:=36;                  kyc.Width:=36;
  kxc.Text:='0,5';

  for i:=0 to n do begin
    kx[i]:=tEdit.Create(form1);     ky[i]:=tEdit.Create(form1);
    kx[i].Parent:=form1;            ky[i].Parent:=form1;
    kx[i].Top:=36+36*i;             ky[i].Top:=36+36*i;
    kx[i].Left:=36;                 ky[i].Left:=72;
    kx[i].Width:=36;                ky[i].Width:=36;
    kx[i].Text:=intToStr(i);        ky[i].Text:=intToStr(i);
  end;
end;

xc is x coordinate where the corresponding y (yc) is obtained using Newton method by calling it

yc=fn(xc)

function tform1.fn(xs:real):real;
var i:integer;fs:real;
begin
  fs:=0;
  for i:=0 to n do begin
    fs:=fs+b(i,0)*c(xs,i);
  end;
  fn:=fs;
end;

the fn function call the two other function. The b function, a recursive contain divided difference like this

function tform1.b(i,j:integer):real;
begin
  if i=0 then b:=y[0]
    else if (i-j)=1 then
      b:=(y[i]-y[j])/(x[i]-x[j])
        else
          b:=(b(i,j+1)-b(i-1,j))/(x[i]-x[j]);
end;

and c function, a recursive function (or you could rewrite it using simple for command)

function tform1.c(xs:real;i:integer):real;
begin
  if i=0 then c:=1
    else c:=(xs-x[i-1])*c(xs,i-1);
end;

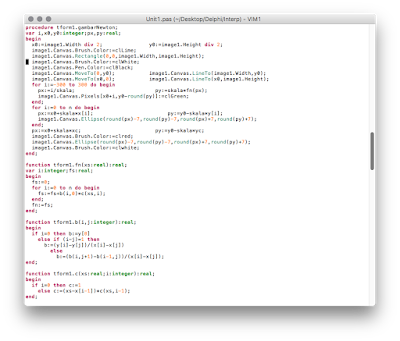
and finally, draw the data and the function on image1

fprocedure tform1.gambarNewton;
var i,x0,y0:integer;px,py:real;
begin
  x0:=image1.Width div 2;               y0:=image1.Height div 2;
  image1.Canvas.Brush.Color:=clLime;
  image1.Canvas.Rectangle(0,0,image1.Width,image1.Height);
  image1.Canvas.Brush.Color:=clWhite;
  image1.Canvas.Pen.Color:=clBlack;
  image1.Canvas.MoveTo(0,y0);           image1.Canvas.LineTo(image1.Width,y0);
  image1.Canvas.MoveTo(x0,0);           image1.Canvas.LineTo(x0,image1.Height);
  for i:=-300 to 300 do begin
    px:=i/skala;                          py:=skala*fn(px);
    image1.Canvas.Pixels[x0+i,y0-round(py)]:=clGreen;
  end;
  for i:=0 to n do begin
    px:=x0+skala*x[i];                        py:=y0-skala*y[i];
    image1.Canvas.Ellipse(round(px)-7,round(py)-7,round(px)+7,round(py)+7);
  end;
  px:=x0+skala*xc;                        py:=y0-skala*yc;
  image1.Canvas.Brush.Color:=clred;
  image1.Canvas.Ellipse(round(px)-7,round(py)-7,round(px)+7,round(py)+7);
  image1.Canvas.Brush.Color:=clwhite;
end;