Newton Polinomial.

Here's code for Newton's divided differences interpolation polynomial (quite mouthful huh, :) ).

The purpose of this method is to create a function (polynomial) that passes through given set of data points.




I read data point from several edit box.

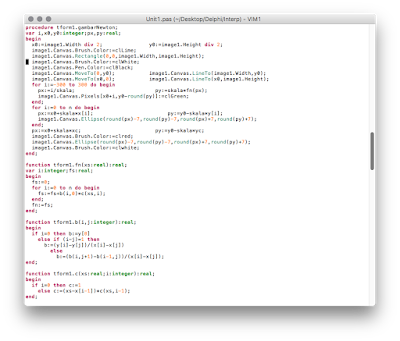
procedure TForm1.Button3Click(Sender: TObject);
var i:integer;
begin
  for i:=0 to n do begin
    x[i]:=strToFloat(kx[i].Text);
    y[i]:=strToFloat(ky[i].Text);
  end;
  xc:=strToFloat(kxc.Text);
  yc:=fn(xc);
  kyc.Text:=floatToStr(yc);
  gambarNewton;
end;

.
kx and ky is tEdit created when button1 is clicked

procedure TForm1.Button1Click(Sender: TObject);
var i:integer;
begin
  button2.Enabled:=true;
  button3.Enabled:=true;
  button4.Enabled:=true;
  button5.Enabled:=true;

  n:=strToInt(edit1.Text);
  kxc:=tEdit.Create(form1);       kyc:=tEdit.Create(form1);
  kxc.Parent:=form1;              kyc.Parent:=form1;
  kxc.Left:=36;                   kyc.Left:=72;
  kxc.Width:=36;                  kyc.Width:=36;
  kxc.Text:='0,5';

  for i:=0 to n do begin
    kx[i]:=tEdit.Create(form1);     ky[i]:=tEdit.Create(form1);
    kx[i].Parent:=form1;            ky[i].Parent:=form1;
    kx[i].Top:=36+36*i;             ky[i].Top:=36+36*i;
    kx[i].Left:=36;                 ky[i].Left:=72;
    kx[i].Width:=36;                ky[i].Width:=36;
    kx[i].Text:=intToStr(i);        ky[i].Text:=intToStr(i);
  end;
end;

xc is x coordinate where the corresponding y (yc) is obtained using Newton method by calling it

yc=fn(xc)

function tform1.fn(xs:real):real;
var i:integer;fs:real;
begin
  fs:=0;
  for i:=0 to n do begin
    fs:=fs+b(i,0)*c(xs,i);
  end;
  fn:=fs;
end;

the fn function call the two other function. The b function, a recursive contain divided difference like this

function tform1.b(i,j:integer):real;
begin
  if i=0 then b:=y[0]
    else if (i-j)=1 then
      b:=(y[i]-y[j])/(x[i]-x[j])
        else
          b:=(b(i,j+1)-b(i-1,j))/(x[i]-x[j]);
end;

and c function, a recursive function (or you could rewrite it using simple for command)

function tform1.c(xs:real;i:integer):real;
begin
  if i=0 then c:=1
    else c:=(xs-x[i-1])*c(xs,i-1);
end;

and finally, draw the data and the function on image1

fprocedure tform1.gambarNewton;
var i,x0,y0:integer;px,py:real;
begin
  x0:=image1.Width div 2;               y0:=image1.Height div 2;
  image1.Canvas.Brush.Color:=clLime;
  image1.Canvas.Rectangle(0,0,image1.Width,image1.Height);
  image1.Canvas.Brush.Color:=clWhite;
  image1.Canvas.Pen.Color:=clBlack;
  image1.Canvas.MoveTo(0,y0);           image1.Canvas.LineTo(image1.Width,y0);
  image1.Canvas.MoveTo(x0,0);           image1.Canvas.LineTo(x0,image1.Height);
  for i:=-300 to 300 do begin
    px:=i/skala;                          py:=skala*fn(px);
    image1.Canvas.Pixels[x0+i,y0-round(py)]:=clGreen;
  end;
  for i:=0 to n do begin
    px:=x0+skala*x[i];                        py:=y0-skala*y[i];
    image1.Canvas.Ellipse(round(px)-7,round(py)-7,round(px)+7,round(py)+7);
  end;
  px:=x0+skala*xc;                        py:=y0-skala*yc;
  image1.Canvas.Brush.Color:=clred;
  image1.Canvas.Ellipse(round(px)-7,round(py)-7,round(px)+7,round(py)+7);
  image1.Canvas.Brush.Color:=clwhite;
end;

Short Function.

Here's my implementation of function according to The Power of 10;

"Restrict functions to a single printed page."

As bonus, I didn't use global variable if possible. So if a function or procedure need a variable from others, it have to be passed using parameter on that function.

If we look at the code below, we know that it can be rewritten using a long single procedure or function. But according The Power of Ten, a function should be as short as possible so it could be printed in a single page.

So, instead one long multiple page function, I write/break it as several short-single-printed-page functions. :)

unit Unit1;

interface

uses
  Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
  Dialogs, StdCtrls;

type
  TForm1 = class(TForm)
    Edit1: TEdit;
    Edit2: TEdit;
    Button1: TButton;
    Edit3: TEdit;
    Edit4: TEdit;
    procedure proses;
    function konversi(a:real;c,d:char):string;
    function konversiC(a:real;d:char):string;
    function konversiF(a:real;d:char):string;
    function konversiR(a:real;d:char):string;
    function konversiK(a:real;d:char):string;
    procedure Button1Click(Sender: TObject);
  private
    { Private declarations }
  public
    { Public declarations }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);
begin
  proses;
end;

procedure tform1.proses;
var
  a:real;
  s,b:string;
  c,d:char;
begin
  a:=strToFloat(edit1.Text);
  s:=edit2.Text;
  c:=s[1];
  s:=edit4.Text;
  d:=s[1];
  b:=konversi(a,c,d);
  edit3.Text:=b;
end;

function tform1.konversi(a:real;c,d:char):string;
begin
  case c of
    'C':konversi:=konversiC(a,d);
    'F':konversi:=konversiF(a,d)
    'R':konversi:=konversiR(a,d)
    'K':konversi:=konversiK(a,d)
    else konversi:='error';
  end;
end;

function tform1.konversiC(a:real;d:char):string;
begin
  case d of
    'C':konversiC:=floatToStr(a);
    'F':konversiC:=floatToStr(a*9/5+32);
    'R':konversiC:=floatToStr(a*4/5);
    'K':konversiC:=floatToStr(a+273);
    else konversiC:='Error';
  end;
end;

function tform1.konversiF(a:real;d:char):string;
begin
  case d of
    'C':konversiF:=floatToStr((a-32)*5/9);
    'F':konversiF:=floatToStr(a);
    'R':konversiF:=floatToStr((a-32)*4/9);
    'K':konversiF:=floatToStr((a-32)*5/9+273);
    else konversiF:='Error';
  end;
end;

function tform1.konversiR(a:real;d:char):string;
begin
  case d of
    'C':konversiR:=floatToStr(a*5/4);
    'F':konversiR:=floatToStr(a*9/4+32);
    'R':konversiR:=floatToStr(a);
    'K':konversiR:=floatToStr(a*5/4+273);
    else konversiR:='Error';
  end;
end;

function tform1.konversiK(a:real;d:char):string;
begin
  case d of
    'C':konversiK:=floatToStr(a-273);
    'F':konversiK:=floatToStr((a-273)*9/5+32);
    'R':konversiK:=floatToStr((a-273)*4/5);
    'K':konversiK:=floatToStr(a);
    else konversiK:='Error';
  end;
end;

end.

.

Another Turtle in Circle

There's always another way to solve something.

So, I have another code for "Turtle in Circle" code, :)

In the script below, I use turtle position to determine if it's still inside circle or not. If it outside circle, instead of send it to zero position, I send it to random position inside circle.

import turtle
from random import uniform
import numpy as np

turtle.shape("turtle")
#turtle.speed(1)
x = 0
y = 0
rmax=40

for i in range (1,1000):
    a = uniform (-90,90) #angle
    turtle.left(a)
    d = uniform (-75,75) #distance
    x = turtle.xcor()+d*np.cos(a*np.pi/180)
    y = turtle.ycor()+d*np.sin(a*np.pi/180)
    r = np.sqrt(x*x+y*y)
    if r>rmax:
        turtle.setx(uniform(-rmax,rmax))
        turtle.sety(uniform(-rmax,rmax))
        x = 0
        y = 0
    else:
        turtle.forward(d)

turtle.exitonclick()



 

.

Turtle in Circle

I use previous code and improve it so the turtle could only move at certain circle area.

import turtle
from random import uniform
import numpy as np

turtle.shape("turtle")
#turtle.speed(1)
x = 0
y = 0

for i in range (1,1000):
    a = uniform (-90,90) #angle
    turtle.left(a)
    d = uniform (-75,75) #distance
    x += d*np.cos(np.pi*a/180)
    y += d*np.sin(np.pi*a/180)
    r = np.sqrt(x*x+y*y)
    if r>40:
        turtle.setx(0)
        turtle.sety(0)
        x = 0
        y = 0
    turtle.forward(d)

turtle.exitonclick()



 

.

Anti MainStream.

Saat booming sepatu roda, Alfa malah sibuk berlatih skateboard, :D .

Random Turtle Movement.

I use turtle module, the standard module, in Python.

The turtle movement has random direction (angle), and random distance (forward/backward).

import turtle
from random import uniform

turtle.shape("turtle")
turtle.speed(1)
for i in range (1,100):
    #random angle
    a = uniform (-90,90)
    turtle.left(a)
    #random move
    d = uniform (-100,100)
    turtle.forward(d)

turtle.exitonclick()



 

.

The Power of 10

Rules for Developing Safety-Critical Code:

Avoid complex flow constructs, such as goto and recursion.

All loops must have fixed bounds. This prevents runaway code.

Avoid heap memory allocation.

Restrict functions to a single printed page.

Use a minimum of two runtime assertions per function.

Restrict the scope of data to the smallest possible.

Check the return value of all non-void functions, or cast to void to indicate the return value is useless.

Use the preprocessor sparingly.

Limit pointer use to a single dereference, and do not use function pointers.

Compile with all possible warnings active; all warnings should then be addressed before release of the software.

https://en.m.wikipedia.org/wiki/The_Power_of_10:_Rules_for_Developing_Safety-Critical_Code